Пусть 
-
традиционное (положительное)
непустое множество. Определим отрицательное множество 
как
результат операции “вычитания” 
из пустого множества 
,
то есть:
=
-
(1)
Физической интерпретацией отрицательного множества является положительное множество, которого уже нет, то есть можно сказать, что отрицательное множество существует в прошедшем времени, тогда как положительное – в настоящем.
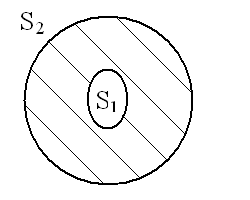
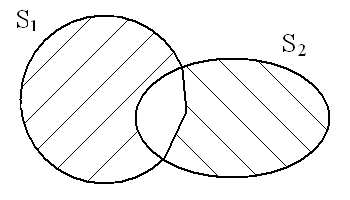
Рис.1 Пример отрицательного множества Рис.2 Пример действительного множества.
На рис.1 показан случай
вычитания множеств 
,
при котором вычитаемое множество
включает в себя то, из которого оно вычитается. При этом результат S
– чисто отрицательное множество, показанное левой штриховкой. В случае, показанном
на рис 2, множество S2 не полностью содержится
в S1 и результирующее множество S
содержит как положительную область ( правая штриховка), так и отрицательная
(левая штриховка на рисунке), что позволяет определить в этом случае S
как действительное множество.
Проиллюстрируем общий
вид действительного множества на примере вычитания двух простейших числовых
множеств: {1,2,3} – {2,3,4,5} = {1, 
,
}. Что
касается свойств отрицательных и действительных множеств, то они полностью
аналогичны свойствам традиционных положительных множеств с учетом знака множества
или его части. Так, например, для объединения или логической суммы действительных
множеств справедливо равенство
S + =
S - 
(2)
Аналогично для логического
умножения (пересечения) положительных и отрицательных множеств справедливо
(по аналогии с положительными и отрицательными числами): 
,
а также 
.
Приведем соответствующие примеры
для числовых множеств: 
и 
.
Будем называть комплексным множеством упорядоченную пару S действительных множеств A и B:
S = {A,B} , (3)
где свойства S заданы ниже. Другая запись комплексного множества:
S = A + B* , (4)
где В* - мнимое множество, определяемое следующим образом:
В* В*
= 
(5)
Легко заметить в определении мнимого множества по результату произведения (5), равного отрицательному множеству, аналогию с определением мнимой единицы i в теории комплексных чисел. Множество А в (4) – реальная часть комплексного множества, а В* - мнимая часть. По определению, мнимое множество может быть как положительным, так и отрицательным мнимым множеством.
Физическая интерпретация мнимого множества – это множество, которого еще нет, то есть оно существует как потенциальное в будущем времени. Таким образом комплексное множество может выражать связь объектов, существующих одновременно в прошедшем, настоящем и будущем.
Геометрическая интерпретация комплексного множества показана на рис.3, где мнимая часть представлена фигурой, ограниченной пунктирной линией.
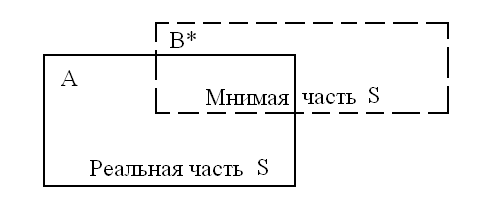
Рис.3. Геометрическое представление комплексного множества S.
Зададим теперь действия над комплексными множествами:
1). Два комплексных
множества 
и
равны
тогда и только тогда, когда 
и
.
2). Сумма двух комплексных множеств
(6)
На рис.4 показана геометрическая интерпретация суммы двух комплексных множеств, все части которых - отрицательные.
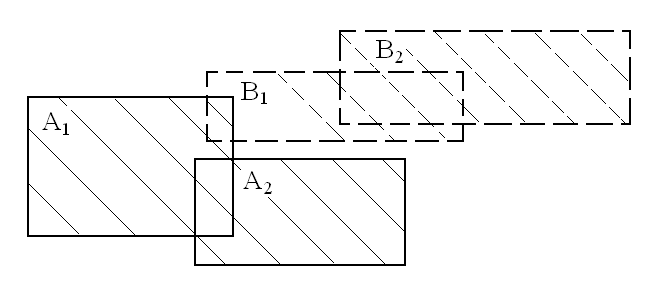
Рис.4. Пример суммы комплексных множеств.
3). Произведение двух комплексных множеств
(7)
определяется аналогично произведению комплексных чисел. Геометрическая интерпретация произведения двух комплексных множеств c отрицательными реальной и мнимой частями показана на рис. 5, где в результате получается чисто действительное множество.
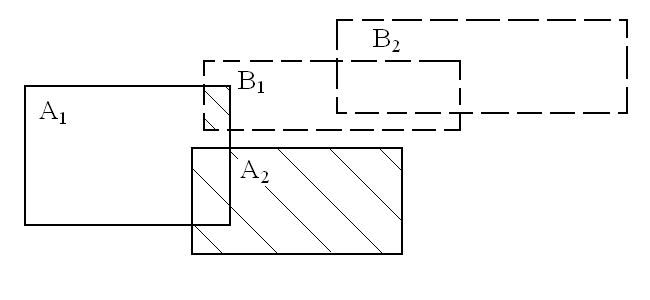
Рис.5 Пример умножения комплексных множеств.
4). Обращение комплексного множества S является результатом обмена местами его реальной и мнимой частей, то есть
S’ = {A,B}’ = {B,A} (8)
Геометрическая интерпретация обращения множеств показана на рис.6.
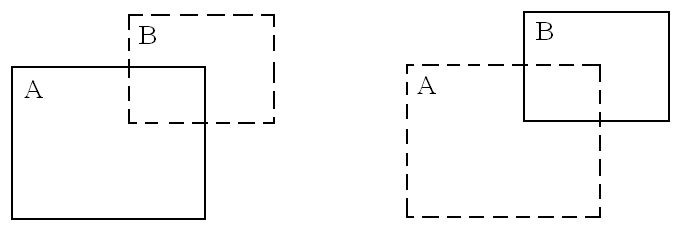
Рис. 6. Пример обращения комплексного множества.
5). Отрицание комплексного множества является результатом изменения знака его частей на противоположный:
(9)
Геометрическая интерпретация отрицания комплексного множества показана на рис.7.
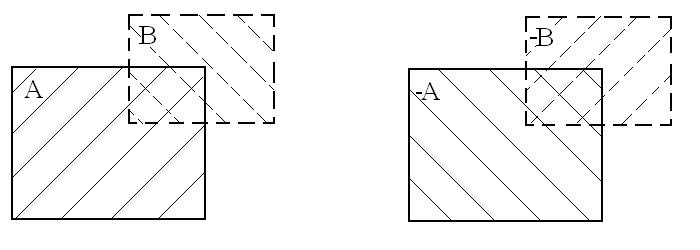
Рис. 7. Пример отрицания комплексного множества.
Традиционное оценивание событий одномерной двоичной логикой с помощью понятий TRUE (истина) и FALSE (ложь) для комплексного случая нуждается в расширении на мнимую область.
Рассмотрим существо предлагаемого подхода [ 3 ] к идентификации комплексных событий на примере простейшего случая двумерной комплексной логики. Специфика в том, что объектом исследования такой логики является субъект (мышление) в традиционном понимании, а субъектом – объект (например, человек). Чтобы разрешить указанное противоречие, объект идентификации рассматривается вместе (в комплексе) с идентифицирующим субъектом, а основой логики такого рассмотрения является комплексное представление ошибки O в виде
O = Re + iIm , (10)
где Re – действительная (продукт человеческого подсознания), а Im – идентифицированная сознанием (мнимая, мысленная) составляющие ошибки. Составляющие ошибки могут присутствовать ( Re, Im = TRUE = 1) или отсутствовать ( Re, Im = FALSE = 0). На основе этого формируются 4 комплексных термина:
ПРАВДОПОДОБИЕ (1 + i1) - утверждение присутствия ошибки (1 принимается за 1);
ЛОЖЬ (0 + i1) - утверждение отсутствия ошибки; (0 принимается за 1)
ИСТИНА (0 + i0) - отрицание отсутствия ошибки (0 принимается за 0);
ОШИБКА (1 + i0) - отрицание присутствия ошибки.(1 принимается за 0) (11)
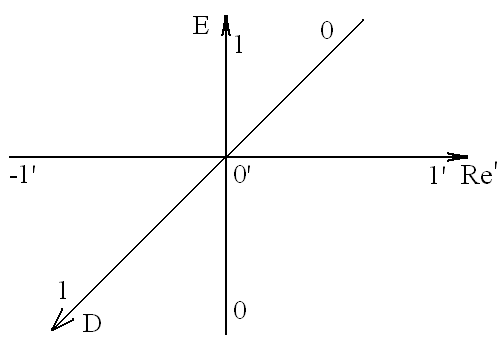
Таким образом, с точки зрения комплексной логики, истинное утверждение отрицает отсутствие ошибки (и в том числе, в нем самом). Приведем геометрическую интерпретацию соответствующих типов событий в двумерной комплексной логике как квадрантов на плоскости (рис. 8):
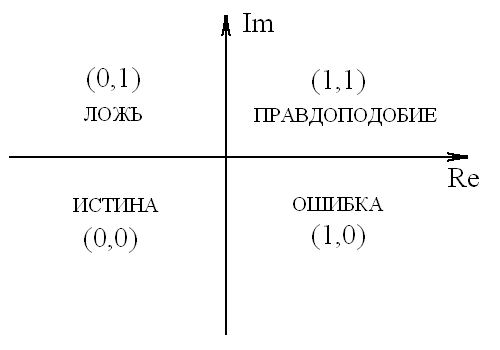
Рис.8. Комплексная плоскость с терминами 4-значной (первичной) комплексной логики.
Физической интерпретацией четырехзначной комплексной логики является мышление человека при работе с компьютерной программой, дающей истинные (TRUE) и ложные (FALSE) ответы в заранее непредсказуемой для субъекта последовательности (например, с вероятностью 50%).
Для построения алгебры комплексных событий необходимо наряду с достоверным 1 и невозможным 0 событиями ввести антидостоверное событие –1, соответствующее всем возможным исходам в отрицательном множестве. Зададим –1 как элемент класса объектов, удовлетворяющих условиям:
А(-1) = -А; А+ (-1) = -1 (12)
Введем теперь алгебру комплексной логики как комплексное множество специального вида, имеющее действительные элементы:
Наибольший элемент 1
Нулевой элемент 0
Наименьший элемент -1 и комплексные элементы, заданные формулой (11).
Алгебра содержит вместе с каждым своим действительным элементом x его отрицание –x, удовлетворяющее соотношениям:
x(-x) = 0, при x = 0
x(-x) = -1 в ином случае;
x + (-x) = 0 (13)
Для действительных элементов 0,1,-1 выполняются операции сложения, вычитания и умножения, заданные в таблице 1:
Таблица 1.
|
Сл. + |
0 |
1 |
-1 |
Выч. - |
0 |
1 |
-1 |
Умн.
|
0 |
1 |
-1 |
|
0 |
0 |
1 |
-1 |
0 |
0 |
-1 |
1 |
0 |
0 |
0 |
0 |
|
1 |
1 |
1 |
0 |
1 |
1 |
0 |
1 |
1 |
0 |
1 |
-1 |
|
-1 |
-1 |
0 |
-1 |
-1 |
-1 |
-1 |
0 |
-1 |
0 |
-1 |
1 |
Таким образом, алгебра первичной комплексной логики для комплексных событий (11) определяется операциями сложения (6), умножения (7), обращения (8) и отрицания (9) комплексных множеств и введенными в таблице 1 операциями над действительными элементами.
